CS log
Dynamic Programming 본문
DP란
메모리 공간을 약간 더 사용하면 연산 속도를 더 비약적으로 증가시킬 수 있는 방법
top down과 bottom up 방식이 있다. + 메모이제이션 기법
대표적인 문제로는 피보나치 수열
이전 두 항의 합을 현재의 항으로 설정하는 수열
점화식(인접 3항간 점화식)을 이용하여 표현하면, a_n+2 = f(a_n+1 , a_n) = a_n+1 + a_n
최종적인 피보나치 수열은

프로그래밍에서는 이를 배열이나 리스트로 표현가능. 수열 자체가 여러 개의 수가 규칙에 따라 배열된 형태를 의미하기 때문이다.
f(n)을 표현할 때 f(2),f(1)은 항상 1이므로 호출을 정지한다. 이를 코드로 표현하면 아래와 같다.
def fibo(n) :
if n==1 or n==2 :
return 1
else : fibo(n-1) + fibo(n-2)
그러나 빅오표기법에 의하면 이 수열은 O(2^n) 시간이 소요된다. 즉, n이 커지면 기하급수적으로 연산량이 늘어나는 것이다. 😱
왜냐하면...
재귀 호출 트리의 구조를 보면, 각 노드에서 두 개의 하위 노드를 생성한다. 이 때문에 호출 트리는 다음과 같이 증가합니다:
- 루트 노드(fibo(n))는 1개,
- 깊이가 1인 노드(fibo(n-1)와 fibo(n-2))는 2개,
- 깊이가 2인 노드(fibo(n-2)와 fibo(n-3) ...)는 4개,
- 깊이가 k인 노드는 2^k개.
트리의 최대 깊이는 n, 따라서 총 노드 수는:
1+2+4+⋯+2n−1
이러한 문제에서 다이나믹 프로그래밍을 사용하면 효율적으로 문제를 해결할 수 있다.
다만, 다이나믹 프로그래밍은 항상 사용할 수 있는 건 아니고 다음 조건을 만족할 때 사용할 수 있다.
1) 큰 문제를 작은 문제로 나눌 수 있다.
2) 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.
메모이제이션은 다이나믹 프로그래밍을 구현하는 방법 중 한 종류. 한번 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법. = 캐싱
한 번 구한 정보를 리스트에 저장하는 것이다. 그리고 한번 저장했던 문제는 답을 저장해놓고, 이 문제는 이미 해결됐던 것이므로 다시 해결할 필요가 없다고 하고 반환하는 것이다.
참고로 퀵 정렬은 정렬을 수행할 때 정렬할 리스트를 분할하며 전체적으로 정렬이 될 수 있도록 한다. 이는 분할 정복 알고리즘으로 분류된다. 다이나믹 프로그래밍과 분할 정복의 차이점은 다이나믹 프로그래밍은 문제들이 서로 영향을 미치고 있다는 점이다.
1) 탑다운 방식 (하향식)
큰 문제를 해결하기 위해 작은 문제를 호출

따라서 시간복잡도는 O(N)이다. 왜냐하면 f(1)을 구한 다음 그 값이 f(2)를 푸는 데 사용되고, f(2)의 값이 f(3)을 푸는 데 사용되는 방식으로 이어지기 때문이다. 한 번 구한 결과는 다시 구해지지 않는다. 따라서 다음과 같이 방문한다.
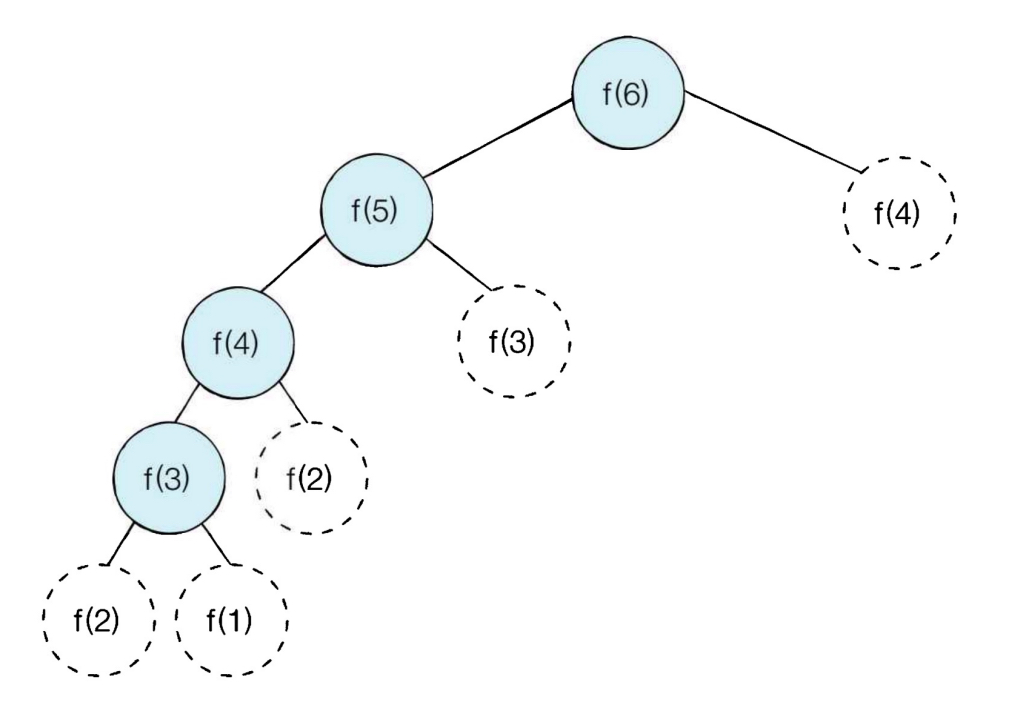
2) 보텀업 방식 (상향식) - 다이나믹 프로그래밍
반복문을 사용하여 아래에서 위로, 작은 문제부터 차근차근 답을 도출한다.

예를 들어 d(3) =d(2) + d(1) 부터 구하므로 d(1)부터 위로 올라가는 방식임을 알 수 있다.
dp는 코테에서 간단한 형태로 출제되므로 완전 탐색 알고리즘으로 접근했을 때 시간이 매우 오래 걸리면 다이나믹 프로그램을 적용할 수 있는지 해결하고자 하는 부분 문제들의 중복 여부를 확인해보자!
'CS > Algorithm' 카테고리의 다른 글
| [백준] 11727번 2xn 타일링 2 (0) | 2025.01.12 |
|---|---|
| [백준] 14501번 (0) | 2025.01.12 |
| [백준/python] 11724 : 연결요소의 개수 (0) | 2024.08.18 |
| DFS & BFS (0) | 2024.08.14 |
| 기초 자료구조 (0) | 2024.08.14 |




