CS log
DFS & BFS 본문
1. DFS/BFS 기초
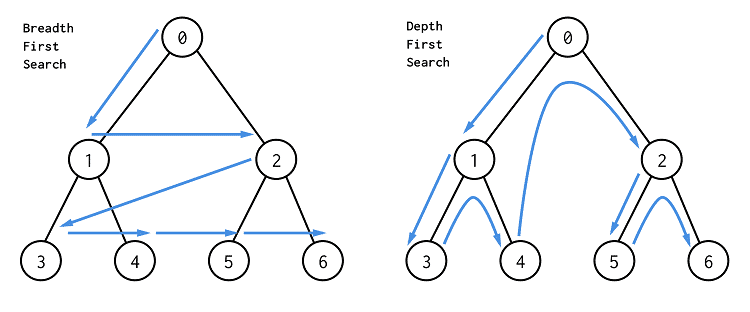
- 공통점
- 그래프를 끝까지 탐색하기 위한 알고리즘이다 (완전탐색)
- to_visit, visited 리스트를 관리하는 것이 핵심이다!
- 차이점
- 탐색 순서 차이
- DFS는 상하로 우선 탐색, BFS는 좌우로 우선 탐색
- 구현상의 차이점 : to_visit을 관리하고자 DFS는 스택, BFS는 큐(deque)를 사용
- codes overview
def dfs(graph, start_node) :
to_visit, visted = list(), list() # stack으로 관리
to_visit.append(start_node)
while to_visit :
node = to_visit.pop()
if node not in visited :
visited.append(node)
to_visit.extend(graph[node]) # 현재 노드 node와 연결된 모든 이웃 노드를 to_visit 스택에 추가
return visited
from collections import deque
def bfs(graph, start_node) :
to_visit, visited = deque(), [] # queue로 관리
to_visit.append(start_node)
while to_visit :
node = to_visit.popleft()
if node not in visited :
visited.append(node)
to_visit.extend(graph[node])
return visited
2. DFS & BFS 변형
1) 지도를 사용하는 경우
def dfs(road, n, m) :
to_visit, visited = [], []
to_visit.append((n,m))
cnt = 0
while to_visit :
n,m = to_visit.pop()
if (n,m) not in visited :
visited.append((n,m))
road[n][m] = 0
cnt+=1
for dn,dm in [(+1,0), (-1,0), (0,+1), (0,-1)] :
if 0<= (n+dn) < N and 0<=(m+dm) <M and road[n+dn][m+dm] == 1 :
to_visit.append((n+dn, m+dm))
return cnt
2) global visited
def dfs(road, n, m) :
to_visit = []
to_visit.append((n,m))
cnt = 0
while to_visit :
n,m = to_visit.pop()
if road[n][m] == 1 :
road[n][m] = 0 # visited list 역할. 방문 처리
cnt += 1
for dn,dm in [(+1,0), (-1,0), (0,+1), (0,-1)] :
if 0<= (n+dn) < N and 0<=(m+dm) <M and road[n+dn][m+dm] == 1 :
to_visit.append((n+dn, m+dm))
return cnt
3) DFS & BFS 확장
백준 1182 - 부분 수열의 합을 dfs로 풀이!
n_nums, target = map(int, input().split())
nums = list(map(int, input().split()))
cnt = 0
def dfs(idx,sum) :
global cnt
if idx >= n_nums : # 재귀함수의 종료 조건 ; 리스트 끝에 도달하면 중지
return
sum += nums[idx]
if sum == target :
cnt += 1
dfs(idx+1, sum)
dfs(idx+1, sum-nums[idx])
dfs(0,0) # idx = 0, sum = 0인 처음의 상태에서 시작
print(cnt)
'CS > Algorithm' 카테고리의 다른 글
| Dynamic Programming (0) | 2025.01.08 |
|---|---|
| [백준/python] 11724 : 연결요소의 개수 (0) | 2024.08.18 |
| 기초 자료구조 (0) | 2024.08.14 |
| [백준/python] 1182번 : 부분 수열의 합 (0) | 2024.08.11 |
| [백준/python] 4779번 : 칸토어 집합 (0) | 2024.08.09 |



