목록2024/08 (12)
CS log
 [백준/python] 11724 : 연결요소의 개수
[백준/python] 11724 : 연결요소의 개수
✔️ 풀이 방법n,m을 받은 후 n*n의 graph 표를 만든다.이후 u와 v를 받아서 어떤 간선끼리 연결되어 있는지 graph에 기록한다.연결 요소의 개수를 구하는 것은 인접한 정점으로 이루어진 그래프 개수를 세는 것과 같다. ✔️ 코드import syssys.setrecursionlimit(10**6)n,m = map(int, sys.stdin.readline().split())graph = [[]for _ in range(n+1)]visited = [False]*(n+1)cnt=0for _ in range(m) : u,v = map(int, sys.stdin.readline().split()) graph[u].append(v) graph[v].append(u)# DFSdef dfs..
 [스프링 입문] 프로젝트 생성
[스프링 입문] 프로젝트 생성
1) 오류A problem occurred configuring root project 'practice'.> Could not resolve all files for configuration ':classpath'.> Could not resolve org.springframework.boot:spring-boot-gradle-plugin:3.0.1.Required by:project : > org.springframework.boot:org.springframework.boot.gradle.plugin:3.0.1> No matching variant of org.springframework.boot:spring-boot-gradle-plugin:3.0.1 was found. The consumer w..
 DFS & BFS
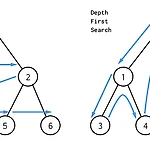
DFS & BFS
1. DFS/BFS 기초공통점그래프를 끝까지 탐색하기 위한 알고리즘이다 (완전탐색)to_visit, visited 리스트를 관리하는 것이 핵심이다!차이점탐색 순서 차이DFS는 상하로 우선 탐색, BFS는 좌우로 우선 탐색구현상의 차이점 : to_visit을 관리하고자 DFS는 스택, BFS는 큐(deque)를 사용codes overviewdef dfs(graph, start_node) : to_visit, visted = list(), list() # stack으로 관리 to_visit.append(start_node) while to_visit : node = to_visit.pop() if node not in visited : ..
 기초 자료구조
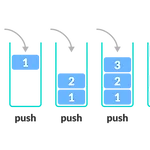
기초 자료구조
1. StackLIFO(후입선출, Last-in First-out)대표적인 stack 자료구조 활용 : ctrl + z 파이썬에서의 구현 ➡️ 리스트stack = []stack.append(1) # [1]stack.append(2) # [1,2]stack.append(3) # [1,2,3]stack.pop() # [1,2] stack 자료 구조의 단점 ? 1 빼려면 2,3을 모두 빼야 함. 시간복잡도가 매우 큼. 맨 안쪽에 있는 블럭을 빼려면 느림. 2. Deque, double-ended queue보통의 큐는 FIFO(선입선출, First-in First-out)뒤에서는 push만, 앞에서는 pop만 가능하다. deque는 앞/뒤 모두에서 push와 pop이 가능하다! python에서의 구현 ➡️ f..
